Hello!

Movie recommendations using Julia

Introduction

Recommender systems have been playing a pivotal role in various business settings like e-commerce sites, social media platforms, and other platforms involving user interaction with other users or products. Recommender systems provide valuable insights to gain actionable
intelligence on these users.

Large Scale Recommender systems help in unraveling the latent information in the complex relational data between users and items. Mapping of the users space to the items space, to predict the interaction is a challenge. Inferring actionable information from variety of data sources collected either implicitly like, click patterns, browser history etc. or explicitly like ratings of books and movies, is what well designed recommender systems do consistently well.

Matrix Factorizations

Depending on the source of information on the users and the items, there are variety of techniques to build recommender systems, each of them having a unique mathematical approach. Linear algebra and matrix factorisations are important to certain types of recommenders where user ratings are available and it is most ideal to apply methods like svd in such cases.

In matrix factorization the users and items are mapped onto a joint latent factor space of reduced dimension f, and the inner product of the user vector with item vector gives the corresponding interaction. Matrix factorization is mainly about a more compact representation of the large training data which is obtained by dimensionality reduction. We want to quantify the nature or the characteristics of the movies defined by a certain number of aspects (factors), i.e we are trying to generalize the information (independent and unrelated ratings matrix) in a concise and descriptive way.

Example :
Let us consider a simple example to figure out how matrix factorization helps in predicting the likelihood of a user liking a movie or not.
For sake of brevity, we have couple of users, Joe and Jane and couple of movies, Titanic and Troll 2. The users and the movies are characterized based on certain number of factors as show in the below tables.

Factors/Movies	Titanic	Troll 2
Romance	4	1
Comedy	2	4
Box Office success	5	2
Drama	3	2
Horror	1	4

Factors/Movies	Joe	Jane
Romance	4	1
Comedy	2	4
Box Office success	5	2
Drama	3	2
Horror	1	4

Consider Joe to be characterized by vector [4 2 5 3 1], which suggests that Joe likes Romance and big hit movies and not so much horror or comedy. Similarly Jane likes comedy horror and she is not very particular about box office success of the movies, neither is she a big fan of romance movies.

The movies Titanic, is a popular romance movie, where as the movie Troll 2, is not so popular and horror comedy. It is intuitively obvious that Joe will end up liking Titanic and Jane will like Troll 2. This is based on how the users and movies score on the 5 factors. Using Cosine distance as shown in the below table, confirms this.
$$\cos(\theta) = \frac{Titanic * Joe}{\|Titanic\|\|Joe\|}$$

Factors/Movies	Joe	Jane
Titanic	0.94	0.67
Troll 2	0.50	0.97

With large rating data matrix, like in the NETFLIX dataset which had around 20 thousand movies and 0.5 million users, mapping all the users and the movies in the above way is impossible. This is where matrix factorization helps in factoring the Rating matrix into user matrix and movie matrix.

Alternating Least Squares

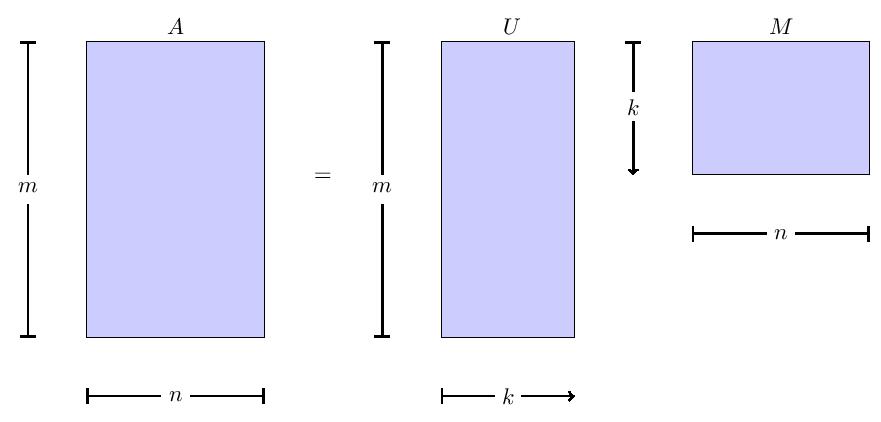
Let $U={u_i}$ be the user feature matrix where ${u_i} \subseteq \mathbb{R}^{n_f}$ and $i=1,2,…,n_u$, and let $M={m_j}$ be the item or
movie feature matrix, where ${m_j} \subseteq \mathbb{R}^{n_f}$ and $j=1,2,...,n_m$. Here $n_f$ is the number of factors, i.e., the reduced dimension or the lower rank, which is determined by cross validation. The predictions can be calculated for any user-movie combination,
$(i,j)$, as $r_{ij}={u_i} \cdotp {m_j}, \forall i,j$.

Here we minimize the loss function of $U$ and $M$ as the condition in the iterative process of obtaining these matrices. Let us start by considering the loss due to a single prediction in terms of squared error:
$$\begin{equation} \mathcal{L}^2(r,{u},{m})=(r-<{u},{m}>)^2. \end{equation}$$

Based on the above equation generalizing it for the whole data set, the
\emph{empirical} total loss as:
$$\begin{equation} \mathcal{L}^{emp}(R,U,M)=\frac{1}{n} \sum_{(i,j) \in I}\mathcal{L}^2(r_{ij},{u_i},{m_j}), \end{equation}$$
where $I$ is the known ratings dataset having $n$ ratings.

Julia recommender system

The package RecSys.jl is a package for recommender systems in Julia, it can currently work with explicit ratings data. The API for preparing the input is creating an instance of ALSWR type, which expects as input parameters input file location. The second optional input is the variable par which specifies the type of parallelism. The default is set to shared memory parallelism, however by passing par=ParThreads(), we could set to multithreaded parallelism.

rec=ALSWR("/location/to/input/file/File.delim", par=ParThread)

The file can be any tabular structured data, delimited by any character, which needs to be specified,

inp=DlmFile(name::AbstractString; dlm::Char=Base.DataFmt.invalid_dlm(Char), header::Bool=false, quotes::Bool=true)

The call to the function to create a model is train(rec, 10, 4) where 10 is the number of iterations to run and 4 is the number of factors.

A log of a test run on the NETLIX data is shown below,

05-Jan 17:07:28:DEBUG:root:loading inputs...
05-Jan 17:07:50:DEBUG:root:time to load inputs: 22.235926866531372 secs
05-Jan 17:07:50:DEBUG:root:preparing inputs...
05-Jan 17:08:00:DEBUG:root:prep time: 9.460721015930176
05-Jan 17:08:25:DEBUG:root:begin iteration 1
05-Jan 17:08:38:DEBUG:root: users
05-Jan 17:08:44:DEBUG:root: items
05-Jan 17:08:44:DEBUG:root:begin iteration 2
05-Jan 17:08:56:DEBUG:root: users
05-Jan 17:09:01:DEBUG:root: items
05-Jan 17:09:01:DEBUG:root:begin iteration 3
05-Jan 17:09:13:DEBUG:root: users
05-Jan 17:09:19:DEBUG:root: items
05-Jan 17:09:19:DEBUG:root:begin iteration 4
05-Jan 17:09:31:DEBUG:root: users
05-Jan 17:09:37:DEBUG:root: items
05-Jan 17:09:37:DEBUG:root:begin iteration 5
05-Jan 17:09:49:DEBUG:root: users
05-Jan 17:09:54:DEBUG:root: items
05-Jan 17:09:54:DEBUG:root:begin iteration 6
05-Jan 17:10:07:DEBUG:root: users
05-Jan 17:10:12:DEBUG:root: items
05-Jan 17:10:12:DEBUG:root:begin iteration 7
05-Jan 17:10:24:DEBUG:root: users
05-Jan 17:10:30:DEBUG:root: items
05-Jan 17:10:30:DEBUG:root:begin iteration 8
05-Jan 17:10:42:DEBUG:root: users
05-Jan 17:10:48:DEBUG:root: items
05-Jan 17:10:48:DEBUG:root:begin iteration 9
05-Jan 17:11:00:DEBUG:root: users
05-Jan 17:11:05:DEBUG:root: items
05-Jan 17:11:05:DEBUG:root:begin iteration 10
05-Jan 17:11:18:DEBUG:root: users
05-Jan 17:11:23:DEBUG:root: items
05-Jan 17:11:23:DEBUG:root:fact time 203.25707387924194
05-Jan 17:12:43:DEBUG:root:rmse time 79.78545188903809
rmse of the model: 0.8593418667702695

As we can see from the above log, that the rmse is 0.8593. This is very good accuracy compared to some of the prize winning models. The timings too are impressive, for data as large as 1 billion ratings.

Apart from methods to model the data and check for accuracy, there are also abilities to make recommendations for users who have not interacted with items, by picking the most likely items the user would interact with. Hence in RecSys.jl we have a fast, scalable and accurate recommender system which can be used to for end to end system. Upcoming would be a demo of such a system with the UI design too done in Julia, which is possible as of today.

Similarity transformation

  This post throws some light on the similarity tranformations and its applications.
 'An eigenvector defines a one-dimensional subspace that is invariant with respect to premultiplication by A.' (1)
Lets first see what is the formal definition of similarity transformation.

QR factorization latex

%!TEX encoding = UTF-8 Unicode
% Author: Abhijith
\documentclass[a4paper,11pt]{article}
\usepackage[utf8]{inputenc}
\usepackage{tikz}
\usepackage{verbatim}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{5pt}


\usetikzlibrary[positioning]
\usetikzlibrary{patterns}
\usepackage[french]{babel}

\begin{document}
\begin{tikzpicture}

\pgfmathsetmacro\x{3}    
\pgfmathsetmacro\y{11}
\filldraw[fill=blue!20] (1,1) rectangle +(\x,\y);
\draw[thin] (1,1) rectangle +(\x,\y);
\node[above] at (.5*\x + 1,\y + 1){$A$};
\draw [thick,|-] (0,12) -- (0,7);
\node[below] at (0,7){$m$};
\draw [thick,-|] (0,6.5) -- (0,1);
\draw [thick,|-] (1,0) -- (2.25,0);
\node[right] at (2.25,0){$n$};
\draw [thick,-|] (2.75,0) -- (4,0);

% X=5
\node[above] at (\x + 2,.5*\y +1){$\boldmath{=}$};

%X=6
\draw [thick,|-] (6,12) -- (6,7);
\node[below] at (6,7){$m$};
\draw [thick,-|] (6,6.5) -- (6,1);
%X=7
\filldraw[fill=blue!20] (7,1) rectangle +(\x,\y);
\draw[thin] (7,1) rectangle +(\x,\y);
\node[above] at (.5*\x + 7,\y + 1){$Q$};
\draw [thick,|-] (7,0) -- (7.9,0);
\node[right] at (7.9,0){$k\leq n$};
\draw [thick,->] (9.1,0) -- (10,0);

%X=11
\draw [thick,|-] (11,12) -- (11,10.8);
\node[below] at (11,10.8){$k\leq n$};
\draw [thick,->] (11,10.2) -- (11,9);

%X=12
\draw[thin] (12,9) rectangle +(\x,\x);
\node[above] at (.5*\x + 12,\y + 1 ){$R$};
\draw [thick,|-] (12,8) -- (13.25,8);
\node[right] at (13.25,8){$n$};
\draw [thick,-|] (13.75,8) -- (15,8);
\draw[fill=blue!20] (15,9) -- (15,12) -- (12,12) -- (15,9);


\end{tikzpicture}

\end{document}

Basic Matrix methods for Data Sciences

This is the plan for a small course I am taking, Basic Linear Algebra and Matrix techniques for data science. 
  
The following techniques will give you an ability to understand complex machine learning techniques better, it is the first step towards becoming a complete ML expert.We will be working hands on the below mentioned applications and many more while learning the math. You will be playing with the data, testing your creative imagination towards finding new dimensions and patterns within it.

1. Vectors and matrices in Data Mining and pattern recognition.

2. Linear regression techniques. Spaces, span, basis, dimensionality.

3. Orthogonality, Least Squares, QR decompostion, SVD

4. Data mining applications:

 4.1 Classification of Handwritten digits.
    4.1.1 How to classify Handwritten Digits
    4.1.2 Classification Using SVD Bases
    4.1.3 Tangent Distance

 4.2 Text Mining
    4.2.2 Preprocessing
    4.2.3 Vector Space Model
    4.2.4 Latent Semantic Indexing
    4.2.5 Clustering

 4.3 Building a recommender system for NETFLIX data. (from the scratch)

Here we have an opportunity to work with a great new open source language called JULIA.

   
 Will be adding few more applications based on machine learning techniques like
 PCA, CCA, Boosting techniques, Reinforcement learning, SVM etc
 depending on the groups interests.  Many more goodies on the cards.

We are supported and guided by experts, researchers and JULIA open source community.

Interested people kindly add your name and mailID and contact number in the below doc:

https://docs.google.com/spreadsheet/ccc?key=0AmTPAEM_gTnadEl1SFFDdlcwQnNvOTVnWG52NDR4T1E&usp=sharing

ALS for low rank matrix approximation

ALS is a way of solving an matrix equivalent of an regular linear least squares problem. In a regular least sqaures problem we solve for Ax=b, i.e., ||b - Ax|| In the case of ALS we try to solve ||R - UM || in frobenius norm. Now we try to reduce ||R - UM||, to the kind ||b - Ax||.

Example:
Let us consider the first row of R, which will have all the ratings given by the
fist user. Let us assume the user has seen movies 1, 213, 315, 1744, 2133, 7044 and
12344, so in a total of 7 movies. Forming a vector of the known ratings for the first
user we have [1 213 315 1744 2133 7044 12344] , let this be denoted by b.
We initialize the M matrix in a particular way, and it has n_m(total number of movies) rows and n_f(reduced factors) columns. The matrix U has n_u(total number of users) rows and n_f columns. For the case of the first user we can form a sub-matrix of M , denote this by M_u . This matrix M_u will have all the rows from M corresponding to the movies seen by the user u, the first user in this case. Let u be the row vector from U corresponding to the considered user, .i.e, first user. Now we have three components b,M_u and u, so we have a regular least squares problem for ||b - Mu||. This is for the first user, we do this for all the users, hence forming the U matrix. since this cant be the final U we need to alternatively continue to solve for U and M.

You could try to just do an SVD on R, and initialize M=S*V', and use this M in ALS, in this case you might not need many iterations as we dont initialize with random values in M. Any approximation method involving random initial values needs a certain minimum number of iterations to tend towards the right values, as we in each iteration minimize the error to a certain extent only. We cant reduce the whole error in just one iteration.

Tutorial on text mining - Introduction Part 1

Well here we would be looking into 'How does textmining work'. As most peaple say textmining is analogous to finding a needle(your search keywords) in a haystack(world wide web). I have followed the book Matrix Methods in Data Mining and Pattern Recognition by Prof. Lars Eldén. The concepts in this tutorial is mainly based on the above book. The problems in datamining can be approached in either statistical or matrix factorization approach. I was fortunate to take the course under Lars, he is the most inspiring teacher I have had.
    Here we would be dealing with the matrix factorization technique. The task of retrieving a relevant tiny bit (relative to the entire domain) of information from large data which might be unstructured is a tricky one. These kind of tasks are also related to Information retrieval. Apart from the popular search engines like google, bing, yahoo.. IR also plays its role in the field of medicine. The medical community produces research articles pertaining to biomedical research at a prolific rate resulting in a very large knowledge bank. With the growth of such important data, the needs of the medical doctors and the like to extract relevant information had triggered research in test mining particularly for the biomedical knowledge domain. With the biomedical text mining there is a big difference with the normal World Wide Web search in that it includes semantics and natural language understanding. I would cover the NLP aspects in the Part 2 on text mining.
         Before going ahead I would mention the topics we would be learning here.
Preprocessing of the documents : Analyzing and Purification of documents, Indexing, Inverted Indexing, Item Normalization, Stop words, Stemming, Text parser.
Vector Space Model : TDM - Term Document Matrix, term weighting scheme, Sparse matrix storage, Query matching - cosine distance measure, Performance modeling - tolerance, Precision, Recall.
Latent Semantic Indexing : Matrix factorization, Low rank approximation, Singular Value Decomposition.
Clustering, NMF - Nonnegative Matrix Factorization, LGK Bidiagonalization.

Will be back!! 

A Cross Product Formula \[\mathbf{V}_1 \times \mathbf{V}_2 = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial X}{\partial u} & \frac{\partial Y}{\partial u} & 0 \\ \frac{\partial X}{\partial v} & \frac{\partial Y}{\partial v} & 0 \end{vmatrix} \]

Apache Mahout - Befitting of the name!!

Well, it was 7 days back that I posted my first elementary question to the Mahout user group, and today I was able to successfully test my first program. Being a first timer in (Java+Eclipse+Maven+Mahout) = JEMM, it me almost a month to get things running. I would like to thank kuba pawloch@interia.pl, Sean Owen and Julian Ortega for your support. 
  Well I dont think there would have been anyone as ignorant as myself with JEMM, as I could'nt find queries as basic as mine. But anyways now I have moved on, and hope to use Mahout on a more serious note. However if there are/will be anyone who has similar issues, I would like to simply share the issues I had with getting mahout running.